真相的解析度：從報表到因果推論——MMM 的資料粒度、識別與欄式資料庫

閱讀對象： 電商零售業決策者、行銷科學家、數據工程主管

關鍵要點

• 行銷組和建模 (Marketing Mix Modeling, MMM) 主要回答的是「增量（Incrementality）」：若資料只剩「全體總花費 × 全體總營收」，旺季同步上升幾乎必然引爆高度共線性（Multicollinearity）。此時，模型很難看清因果關係。若要把它拆開，必須仰賴數據在時間、地理或產品線上的可用變異（Variation），才有機會識別各渠道的真實因果貢獻。

• 彙總並非無損壓縮，而是刪除「識別能力」，而且不可逆：把聯合資訊（Joint Information）彙總成邊際報表（Marginal Reports）屬於數學上的多對一映射。就像將不同顏色的黏土揉成一團，無法回復鮮明各色；維度一旦被摺疊，藏在裡面的因果線索也將一併消失，後續再堆多複雜的模型，推測也將失去可信證據。

• 欄式資料庫是「保留明細」的底座：現代欄式儲存（Columnar Storage）透過邏輯列對齊（Logical Row Alignment）與元組重組（Tuple Reconstruction），在不預先彙總的前提下，按查詢需求重建任意維度的聯合資料；再以向量化執行（Vectorized Execution）降低 I/O 成本，使大量分析工作跑得動。

• 最低可交付資料規格（MVP Data Spec）：MMM 專案最常「死在起跑線之前」，因為資料連最小單位都湊不齊——缺乏一張同列對齊（Row-aligned）的 Geo × Time（或 Segment × Time）建模表。所謂「同列對齊」，就是同一列必須同時包含 KPI、媒體投放與控制變數；否則只要改用「事後用營收佔比去分攤花費」來補洞，就會把花費變成營收的函數，直接引入嚴重的內生性偏誤，讓模型把結果當原因。

  
  

前言：當數據被彙總，歸因便開始失真

在電商零售的檔期結案會議裡，常見兩份「都很漂亮」的報表：行銷端顯示社群廣告花費 500 萬、平台歸因（Attribution）轉換數亮眼；營運端則顯示北區門市營收顯著成長。

但會議室往往在管理層提出核心戰略問題時陷入沈默：「這筆 500 萬的社群預算，對北區線下營收的『增量』到底是多少？如果把同樣的錢移到南區，預期會怎麼變？」

這個問題之所以難以回答，因為資料早在「彙總」那一步，把最關鍵的連結切斷了：媒體（渠道）與結果（KPI）在同一個可對齊粒度上的聯合資訊（Joint Information）不存在。證據不在，模型再大也只能猜；猜得再自信，也只是猜。

本文將從資訊理論出發，說明為何邊際報表不足以支撐高階行銷組合建模（Marketing Mix Modeling, MMM）；並探討現代資料工程如何透過欄式儲存與向量化執行，把「明細」從成本，變成可以反覆使用的資料資產。

1. 數學上的多對一映射與資訊遺失

在談資料架構之前，必須先承認一個數學事實：把資料從「聯合分佈」彙總為「邊際分佈」，是一個多對一映射（Many-to-one mapping），在數學上不可逆。不可逆的意思並非「目前技術做不到」，而是「資訊在彙總那一刻就被刪掉了」。

1.1 資料處理不等式（DPI）：後處理無法還原真相

從資訊理論的角度，可以把資料處理流程寫成一個馬可夫鏈（Markov Chain）：

原始明細 (X) → 彙總報表 (Y) → 決策推論 (Z)

其中：

• X：原子級明細資料（The Truth）——事件、訂單、曝光、花費等，以地理與時間為鍵可對齊的原始結構。

• Y：經過彙總、平均、分組後的報表（The Report）。

• Z：基於報表做出的推論或決策（The Inference）。

資料處理不等式（Data Processing Inequality, DPI）指出，三者之間的互資訊（Mutual Information）滿足：

I(X; Z) ≤ I(X; Y), 含義很直接，也很殘酷：後處理不會把資訊變多。

換句話說，當系統把「每一筆訂單／每一次曝光的細節」壓成「各區總營收」，若「渠道 × 區域 × 時間」這類聯合結構在彙總時被捨棄，後續再疊多少厲害的模型都不會把那段因果關係算回來——因為它已經不在資料裡了。[1]

（註：DPI 講的是「資訊量上限」，而非自動保證「因果可識別」。因果識別仍需要結構假設與可用變異；只是彙總會先把可用的識別能力砍掉一大截，連談假設的空間都消失了。）

當未知量的自由度大於已知約束、導致「同一份邊際資訊對應多種可能的聯合結構」時，在數學上即屬欠定（Underdetermined）。

1.2 兩張面孔，同一個謊言（欠定系統示例）

為了具體呈現欠定如何發生，此處的例子只談數學結構。

(註：此處以接觸點／平台歸因為例，只為展示聯合資訊被切斷的數學結構；MMM 真正要估計的是對 KPI 的增量效應。)

假設資料庫輸出兩張獨立邊際報表：

• 報表 A（渠道邊際）：Search 10,000，Social 8,000

• 報表 B（區域邊際）：北區 9,000，南區 9,000

看似資訊很多，實際上聯合結構仍可能完全不同。以下兩個截然不同的真實情境，會產出一模一樣的邊際報表：

【情境一：Social 是北區的主力推手】

區域 \ 渠道	Search	Social	區域總計 (邊際)
北區	1,000	8,000	9,000
南區	9,000	0	9,000
渠道總計	10,000	8,000	18,000

【情境二：Social 南北平均，並不突出】

區域 \ 渠道	Search	Social	區域總計 (邊際)
北區	5,000	4,000	9,000
南區	5,000	4,000	9,000
渠道總計	10,000	8,000	18,000

結論： 邊際報表完全一致，但「北區 × Social」的交集可以是 8,000，也可以是 4,000。這代表聯合分佈在邊際之下無法被唯一識別；若只靠彙總報表做歸因，只能做沒有科學根據的猜測。

2. MMM 的必要條件：以變異解決識別問題

既然彙總資料無法還原真相，那麼 MMM 到底需要什麼樣的資料？答案指向統計學的核心：識別（Identification）。

2.1 變異（Variation）是模型的燃料

MMM 不是魔法，本質是利用觀測到的波動去拆解因果關係。

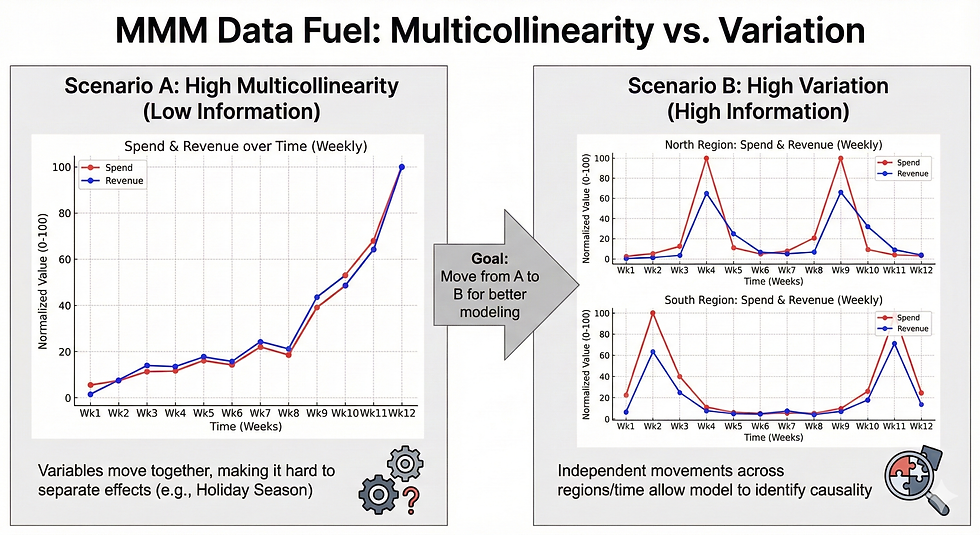
1. 共線性的困境：若只有「全台總 Social 花費」與「全台總營收」，在 Q4 旺季兩者同步上升非常常見。結果是：模型無法分辨「是廣告推高營收」或「旺季推高兩者」。就算勉強算出係數，係數之間的數值也不穩定、標準誤非常大。

2. 可用於識別的差異：當資料具有「空間 × 時間」的差異（例如某段時間北區加碼、南區相對不變），就能在控制季節性、促銷、價格等因素後，讓媒體變數在解釋 KPI 時有更清晰的訊號來源。

3. Geo-level 建模的價值：將 National-level 的單一時間序列（約 T 個觀測）擴張為 Geo-level 的面板資料（約 G × T 個觀測），不僅是為了「資料更大」而已，也是為了讓模型擁有更多可比對的橫截面差異。[2][3]
   

2.2 最低可交付規格（MVP Data Spec）

高階 MMM 需要的是一張具備 Geo × Time（或 Segment × Time） 粒度、且同列對齊（Row-aligned）的聯合資料表。

變數類別	關鍵欄位	對齊要求（Row Alignment）	說明
索引鍵	date（或 week）、geo_id	同一列可對齊	例如：2024-W01 × 台北市
KPI	revenue、conversions	同列對齊	該時空單位的結果變數
媒體變數	spend、impressions	同列對齊	該時空單位的真實投放（避免「全體總數再分攤」）
控制變數	temperature、promo、price、holiday…	同列對齊	影響銷量但非媒體造成的因素

若資料管線只能提供「切斷關聯」的彙總表（例如：有分區營收，但媒體花費只剩全體總額），因為資料先把識別能力拆了，MMM 就很難談增量。

3. 工程上的物理瓶頸：為什麼「多維度細節」這麼難撈？

多維度資料之所以難取得，常見瓶頸分兩層：上游平台 API 與 下游儲存／查詢。

3.1 上游：API 的非同步報表與聚合限制

廣告平台的原始資料本質上是海量事件日誌。當 API 請求帶入複雜 Breakdown（例如 Campaign x Region x Placement），平台端需要做昂貴的聚合運算。為了守住系統穩定性，常見做法是：

• 強制走非同步（Async Jobs）報表流程。

• 對維度組合、回傳列數、時間跨度設上限。

• 因此，多維度資料是權衡算力成本與平台規則的實現。
  

3.2 下游：傳統列式儲存（Row-Based）的 I/O 放大

即使資料成功拉回企業端，若落在偏線上交易處理（Online Transaction Processing, OLTP）取向的 row-store（例如 MySQL／PostgreSQL 的常規表設計），分析查詢通常會遇到 I/O 放大：[4]

• 列式儲存以「列」為單位連續存放；查詢只需要少數幾個欄，仍可能被迫搬運大量無關欄位。

• 結果是快取被無效資料塞爆、查詢延遲飆升，最後逼得系統「只好先彙總」——而彙總一旦提早發生，就回到本文開頭所說的不可逆。
  

4. 欄式儲存與向量化：現代歸因的物理基礎

現代數據棧引入欄式儲存（Columnar Storage；如 BigQuery、Snowflake、Redshift）就是為了解這個矛盾：保留明細，但查詢仍然要快。

4.1 邏輯對齊與元組重組（Logical Alignment & Tuple Reconstruction） 欄式儲存並非把資料預先算成邊際分佈，而是改變資料佈局：把欄位分開存，並以 row group / metadata 維持「同一筆紀錄」在邏輯上的對齊。

以 Parquet/類 Dremel 架構為例（概念化描述）：[5]

• channel 欄：[Search, Social, …]（以 row group 切塊）

• region 欄：[North, North, …]（同一個 row group 對應同一批 row）

查詢引擎做 projection（投影） 時只讀需要的欄；需要還原成「列」時，再做 tuple reconstruction（元組重組） 把欄位拼回同一筆紀錄。對巢狀資料，則靠 definition/repetition levels 等中繼資訊維持記錄邊界與對應關係。

重點只有一句：欄式儲存延後彙總，不犧牲明細；而聯合資訊仍可被重建。

4.2 向量化執行（Vectorized Execution） 欄式儲存的第二個關鍵，是執行方式。向量化查詢引擎會以「一批資料」為單位運算，而非逐列解譯：[6]

• 批次掃描、批次過濾（masking）、批次聚合。

• 更容易吃到 CPU cache 與 SIMD（Single Instruction, Multiple Data）的好處。

• 在分析型工作負載下，有機會把效能提升一到數個數量級（視資料分區、壓縮率、選擇度而定）。

因此，「保留明細」不必然等於「查詢很慢」。慢的通常並非明細本身，而是沒有合適的儲存與執行模型。

5. 結語：從「紀錄」轉向「資產」

對電商零售而言，MMM 的導入不只是建模專案，更是一場對資料的徹底重整：把「看完就算的報表」升級成「可反覆提問、可支撐因果推論的資產」。

為了推進決策，企業可採兩條路徑並行：

1. 快速啟動（Quick Win）：優先盤點並清洗出符合 MVP Spec 的 Geo × Time 歷史資料，先做一輪試算與可行性驗證（Pilot）。

2. 長期建設（Scale Up）：以雲端欄式倉儲作為事件資料底座，保留原始 events，延後彙總，讓未來能回答更細、更狠、更挑釁的歸因問題。

必須認清的殘酷現實：若只剩下彙總過的報表，已經不是企業的資產，只能稱為紀錄的殘影。

附錄 A：MVP Data Spec Checklist（可直接交付資料團隊）

檢核項目	欄位要求	理由
共同 Keys	geo_id + date/week	同一列必須可對齊，這是建模的最小單位。
KPI	至少一個主要 Outcome	如營收（Revenue）、訂單（Conversions）。
Media	每渠道至少一項可量測投入（spend 或 impressions）	必須能落到 Geo × Time。避免用全體總花費按營收佔比回推（見附錄 B）。
Controls	外部變數同列對齊	促銷、天氣、假期、價格、庫存等，需對應到相同的 Geo × Time。

附錄 B：常見缺資料情境與 MMM 風險

情境 (What you have)	缺少的東西 (What’s missing)	對 MMM 的直接風險 (Risk)
只有全體 Spend & Revenue	地理/產品線差異	共線性死結：廣告與季節性共同上升，係數漂移、區間膨脹，結論不可用。
有分區 Revenue，但 Spend 只有全體	媒體的地理差異	識別失敗：只能假設廣告效果在各區一致，失去利用區域差異校準增量的能力。
用「營收佔比」分攤 Spend	真實媒體投放量	內生性偏誤（Endogeneity Bias）：花費成了營收的函數（營收高→分攤多），模型會把結果當原因，係數虛高、決策被帶走。

參考文獻

1. Cover, T. M., & Thomas, J. A. (2006). Elements of Information Theory. (DPI 與互資訊理論) 資源連結：Wiley Online Library

2. Google for Developers. Meridian: Model specification & Input data. (Geo-level 與資料需求) 資源連結：Official Documentation

3. Meta / Facebook Experimental. Robyn Documentation. (MMM 實務框架與資料需求) 資源連結：GitHub Pages

4. Abadi, D. et al. (2008). Column-Stores vs. Row-Stores: How Different Are They Really? (比較儲存架構與執行模式) 資源連結：MIT CSAIL

5. Melnik, S. et al. (Google). (2010). Dremel: Interactive Analysis of Web-Scale Datasets. (欄式儲存、Record Assembly、Repetition/Definition Levels). 資源連結：Google Research

6. Boncz, P., et al. (2005). MonetDB/X100: Hyper-Pipelining Query Execution. 這篇是分析型資料庫（OLAP）領域的奠基之作，它解釋了為什麼現代資料庫（如 Snowflake, BigQuery, ClickHouse）在處理海量數據時能這麼快。資源連結：CIDR DB